Presented to The Developing Group 3 Jun 2006
(An earlier version, Thinking Networks I, was presented on 5 June 2004)
Our aim is: “To get you to think networks. It is about how networks emerge, what they look like, and how they evolve. … Networks are present everywhere. All we need is an eye for them.”
Albert-László Barabasi Linked, p. 7
Contents
1. Introduction
2. Components of Network Theory
3. Key Features of Networks
a. Pattern of organisation
b. Interconnectivity
c. Irreversibility
d. Nonlinearity
e. Unpredictability
f. Dynamic equilibrium
g. The rich grow extraordinarily richer
h. The butterfly effect
i. The inverse butterfly effect
j. No one is in control
4. Further Reading
Note
There are three types of description in this paper:
i. Paragraphs like this are my summary of some of the key concepts in network theory. Words in bold are the key concepts and are followed by a popular definition. Words in curly brackets are alternate descriptions/metaphors, e.g. links {ties, bonds, connections}.
ii. Quotations are indented. Italics are in the original, bold is my addition.
iii. [JL: Words in square brackets are my attempt to use network theory to explain and guide the personal change process.]
1. Introduction
I’ll start with a tribute to Fritjof Capra who made an early and significant contribution to bringing the importance of networks to my attention when he asked:
“Is there a common pattern of organization that can be identified in all living systems? … this is indeed the case. Its most important property is that it is a network pattern. Whenever we encounter living systems … organisms, parts of organisms, or communities of organisms — we can observe that their components are arranged in network fashion. Whenever we look at life, we look at networks.” The Web of Life, p. 81-82
The kinds of networks we shall be considering are complex adaptive or complex dynamic networks.
Complex, not necessarily because of the number of links and nodes, but because of the intricacies of the interconnections. The collective behaviour of a complex adaptive network is not just more than the sum of the parts, it’s something entirely different.
Adaptive, because these networks respond to external and internal events and therefore they are always changing — they are dynamic — both at any moment and over periods of time.
Although adaptation is a signature of organic networks, mechanical and social networks adapt too. The internet for instance automatically responds to the addition or removal of a link or node by re-routing messages via new nodes and links or around failures; and the users of the World Wide Web (www) spread the news of the arrival of a better search engine called Google like wildfire. In other words, complex adaptive networks are intelligent.

However, none of this would be very interesting if it wasn’t for the fact that inspite of their complexity, inspite of the adaptive and dynamic nature of these networks, recent research has shown them to have remarkably consistent patterns of organisation.
To understand the science of networks you have to think differently about the world — and that, in my opinion, is the main reason for a facilitator to study network theory. Time and again netwrok researchers emphasise that in order to think in terms of networks, a new way of thinking is required:
“We’re accustomed to thinking in terms of centralized control, clear chains of command, the straightforward logic of cause and effect. But in highly interconnected systems, where every player ultimately affects every other, our standard ways of thinking fall apart.” Sync, p. 34-35
“The resulting small worlds are rather different from the Euclidean world to which we are accustomed. … Navigating this non-Euclidean world repeatedly tricks our intuition and reminds us that there is a new geometry out there that we need to master in order to make sense of the complex world around us.” Linked, p. 40
“When it comes to large-scale coordinated social action, hindsight is not 20-20 — in fact it can be actively misleading. … The small-world phenomenon is so counterintuitive – it is a global phenomenon, yet individuals are capable only of local measurement.” Six Degrees, p. 53 & 83
“What makes this paradoxical is that you might think that strong social links would be the crucial ones holding a network together. But they aren’t; in fact they are hardly important at all. … We are continually surprised [because] the long-distance social shortcuts that make the world small are mostly invisible in our ordinary social lives. We can only see as far as those to whom we are directly linked.” Nexus, p. 41 & 55
Before we delve into the features of complex adaptive networks let’s take a brief look at the fundamental concepts of network theory–
2. Components of network theory
In network theory the key concepts are structure and dynamics. A network’s structure consists of a configuration of nodes connected together by links into definable clusters. You need to take a snapshot of the network to see it’s structure.
Nodes are identifiable parts of a system. They can be physical (e.g. individual computers or humans) or virtual (e.g. particular web pages or beliefs).
Links represent whatever happens between nodes. Links operate on two levels: physical and informational. The physical medium (e.g. roads or telephone cables) makes the transfer of information possible (e.g. volume of traffic or messages between computers). Links are also known as ties, bonds and connections.
Clusters are groups of nodes that are inter-linked into a unit. The great majority of interactions between nodes is contained within the group. Most people’s friends are also friends of each other. Clustering breeds redundancy (multiple pathways between nodes) which keeps the network going when nodes or links fail, but it also breeds parochialism — it keeps local events local and prevents them from escaping into the rest of the network.
Dynamics has two meanings:
“The first meaning is what we might call dynamics of the network. In this sense of the word, dynamics refers to the evolving structure of the network itself, the making and breaking of network ties. … A dynamical view of networks, claims that existing structure can only be properly understood in terms of the nature of the processes that led to it. The second meaning, is what we might call dynamics on the network. From this perspective, we can imagine the network as a fixed substrate linking a population of individuals, but now the individuals are doing something — the outcome of which is influenced by what their neighbors are doing and, therefore, the structure of the network. … In the real world, both kinds of dynamics are going on all the time. … The structure of the network could change, but so could the pattern of activity on the network.” Six Degrees, p. 54-55
Certain configurations of nodes and links have been identified as signatures of complex adaptative networks.
Nodes are either just nodes or they are hubs – exceptionally large nodes in terms of the number of other nodes they are connected to. Hubs {‘keystone species’ in ecology and ‘connectors’ in sociology} are not just well connected – they are massively connected. e.g.
“90% of all documents on the web have 10 or fewer links pointing to them, while a few, about 3, are referenced by close to a million other pages.” Linked, p. 58
Links can either be weak or strong depending on the amount of interaction between two nodes. Weak links can also be local or long-distance. Local and distant are metaphors. In network theory they do not represent physical distance, they are a measure of interconnectivity. Local links are those within a cluster and long-distance links connect clusters.
That means there are three types of links:
Strong and Local – high interaction between two nodes within a cluster. This is where most of the action takes place, say between good friends.
Weak and Local – low interaction between two nodes within a cluster. These links make up the majority of the network, say between you and your neighbour’s or work colleagues.
Weak and Distant– low interaction between nodes in different clusters. These “weak ties”(Mark Granovetter) or ‘shortcuts’ are the ‘bridges’ that bind a network together and create small worlds. This means they are also an expression of the relationship between the individual and the group level, even though the individuals at the ends of a weak tie will rarely be aware of the role they are playing, say between you and an acquaintance in another country.
[Note: The fourth category ‘Strong and Distant’ links, do not exist because in network theory if two nodes are strongly connected they are automatically part of the same cluster and therefore ‘local’.]
A measure of the connectedness of a network is the average minimum path length (number of links or hops) between any two points. This is know as the degree of separation:
“The ‘average pathlength,’ formalizes the intuitive idea of degrees of separation. To calculate it, take any pair of nodes and count the number of links in the shortest chain between them; then repeat for all other pairs of nodes, and average the resulting chain length. … The average amount of overlap in a network is quantified by a second statistic, the ‘clustering,’ defined as the probability that two nodes linked to a common node will also be linked to each other. … Average pathlength reflects the global structure; it depends on the way the entire network is connected, and cannot be inferred from any local measurement. Clustering reflects the local structure; it depends only on the interconnectedness of a typical neighborhood, the inbreeding among nodes tied to a common center. Roughly speaking pathlength measures how big the network is, clustering measures how incestuous it is.” Sync p. 239-241
As you will see below, to grasp the significance of the ideas emerging from network theory you need to grasp the central role played by hubs and weak ties. Hubs will inevitably have all three types of links and therefore they are importance not just because of their size but also because of the central role they play in the architecture of a network. Weak ties are what make a ‘small world’ small.
It seems that complex adaptive networks are almost always what is known as small-world networks. That is they are highly clustered and highly interconnected at the same time. e.g. the brain has lots of local interconnections, it is discernibly modular, and it has a few long distant connections that link the clusters and make the network an integrated whole. (Gerald Edleman calls the weak links in the brain “re-entrant pathways”). The result is that small-world networks have a surprisingly low degree of separation.
“What distinguishes a small-world network is not only that it has a low number of degrees of separation but also that it remains highly clustered. We might say that the fabric of the network is densely weaved, so that any element remains comfortable and tightly enmeshed within a local web of connections. Consequently, the network overall can be viewed as a collection of clusters, within which the elements are intimately linked, as in a group of friends. A few ‘weak’ links between clusters serve to keep the whole world small. … On the other hand, there are drawbacks to too much clustering. … At its core lies the idea that too much order and familiarity is just as bad as too much disorder and novelty. We instead need to strike some delicate balance between the two.” Nexus, p. 199-207
There are two kinds of small-world network, “egalitarian and aristocratic” (Mark Buchanan), i.e. those without hubs and those with hubs.
In egalitarian networks most of the nodes have approximately the same number of links. Examples are: road, rail and air networks; the electrical power grid and other distribution networks; the network of synchronising fireflies; the neural network of the nematode worm and the human brain.
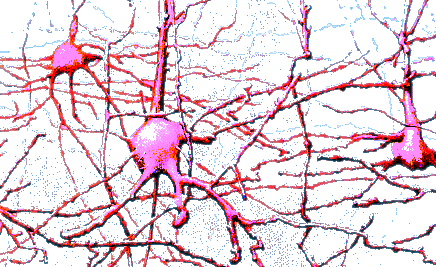
A NEURAL NETWORK
In aristocratic networks a few elements – hubs – have a disproportionally large number of links (see below: power law distribution). Examples are: The Internet and the World Wide Web; ecosystems, food webs and the metabolic network of cells; the networks of individual airline companies; the networks of references in scientific papers and of the co-authors of those papers; networks of directors of major corporations and sexual partners; and the closeness of words used in English sentences.
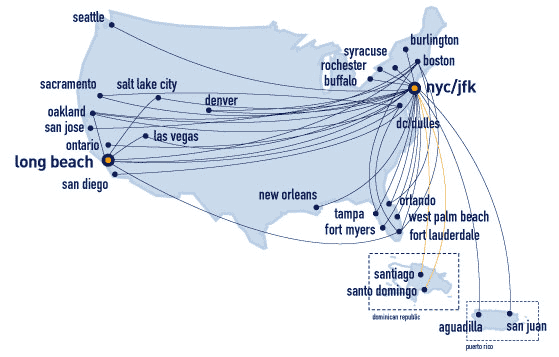
AN AIRLINE NETWORK
A few caveats to bear in mind.
Whenever considering ‘a network’ it is worth remembering that a network is a construct {map, model, metaphor} created by someone to make sense of some aspect of the world. A network comes into existence when someone conceives of some bits of the world as a network – and usually draws a map of their conception. There is no network of species or even World Wide Web pages but it currently seems like a useful way to understand the interactions between living things or how the WWW is interconnected.
This stuff is so new (all the popular books on network theory have been published in the last ten years) that there are bound to be major revisions. It really is ‘work in progress’.
“Claiming that everything is a small-world network or a scale-free network not only oversimplifies the truth but does so in a way that can mislead one to think that the same set of characteristics is relevant to every problem. If we want to understand the connected age in any more than a superficial manner, we need to recognize that different classes of networked systems require us to explore different sorts of network properties.” p. 304 Six Degrees.
[JL And how do we do that? We use bottom-up modelling]
Except where there are physical entities that are physically connected together, all talk of nodes, links, weak and strong ties, hubs and connectors is metaphor. And for every aspect that a metaphor illuminates, it hides something else in shadow.
Because the study of networks is such a new field and because many of the researchers have different scientific backgrounds there are many terms for similar phenomenon. I have tried to reflect this by giving several of the most commonly occurring names. Also, the terminology of networks can be mapped onto the terminology we use in Metaphors in Mind:
COMPARING TERMINOLOGY: LEVELS OF ORGANISATION
| NETWORK THEORY | SYMBOLIC MODELLING |
| Network | Metaphor Landscape |
| Cluster | Perception |
| Links | Relationships |
| Nodes |
Components / Symbols |
3. Key features of networks
Thinking in terms of networks requires you to suspend your common-sense thinking and everyday intuitions, and instead to adopt another set of assumptions {filters, beliefs, metaphors} based on:
a. Pattern of Organisation
b. Interconnectivity
c. Irreversibility
d. Nonlinearity
e. Unpredictability
f. Dynamic equilibrium
g. The rich grow extraordinarily richer
h. The butterfly effect
i. The inverse butterfly effect
j. No one is in control
a. Pattern of Organisation
A surprising discovery about complex adaptive networks is that much of their behaviour has little to do with:
– What the parts are made of
– The behaviour of individuals or parts
– The psychology or intention of individuals
– The history of individuals or parts
Instead network behaviour is more to do with its pattern of organisation – the architecture of the network.
“The interactions between the parts of a complex network often lead to global patterns of organization that cannot be traced to the particular parts. Network architecture is not a property of parts but of the whole.” Nexus, p. 185″
Although the structure of the relationships between a network’s components is interesting, it is important principally because it affects either their individual behavior or the behavior of the system as a whole.” Six Degrees, p. 28
b. Interconnectivity - You are more connected than you think
While one of the famous Stanley Milgram experiments gave birth to the notion that any two humans are connected by six degrees of separation, the brains of all mammals show an even greater connectivity:
“In the cat brain, for example, the number of degrees of separation turns out to be between only two and three. The number is identical in the macaque brain” [Nexus, p. 65].
This might be expected from brains because: (a) it could be life-threateningly dangerous for a message to need to wander around a brain looking for a connecting pathway; and (b) brains have had millions of years to hone their efficiency. However the internet is just a few decades old. Even so, given the number of computers on the internet is over 100 million, an average of just 10 hops to get between any two of them is still pretty small. And given that most people rarely want to connect to a computer hidden in a remote corner of the internet, the typical number of actual hops is more like 4.
Small-world networks are more highly connected than you might expect because:
As the number of links grows the number of pathways through the network grows at a compound rate which is hard for us to comprehend. I don’t know if the mantra “there are more potential pathways in a human brain than particles in the known universe” is true but it makes the point.
Where hubs exist, they will be linked to an unexpectedly high proportion of the network. Hubs are not necessarily ‘big’ nodes (a species of plankton may be a hub in a food web), but they are massively interconnected.
Weak ties that connect distant clusters act as bridges between otherwise unconnected parts of the network. A surprisingly few weak ties create massive interconnectivity. It only takes 200 random links to be added to a network of 6 billion nodes where everyone is linked to their nearest 50 neighbours, for the degree of separation to fall from 60 million to five.
Generally, a node can only ‘see’ the nodes it is connected to – everything outside is invisible. Therefore, for all we know, a person we are not directly connected to may be only two hops from us or they may be a hundred links away.
The take-home message is: Small-world networks have nearly as high a connectivity as a fully-interconnected network (one degree of separation) but with a reduction in the number of links by a factor of thousands. In fact, with a small-world architecture, the larger the network, the proportionally fewer links are required for almost full interconnectivity. The corollary of this is that: (a) adding just a few random long distant links to a network with a high degree of separation, or with isolated clusters, will drastically improve its connectivity; and (b) once the initial few weak ties are in place adding more doesn’t necessarily increase the connectivity of the network.
[JL: It is my guess that symbols in a Metaphor Landscape will likely be as interconnected as any physical ecosystem. This means that any two symbols or ideas will be connected by a maximum of two or three links. In other words you can get from anywhere in your mind to anywhere else is just a few hops. Of course, just because there is a pathway doesn’t mean you can always find it when you need it!
This implies that, if a network is fragmented, only a few extra links are needed to produce high interconnectivity — and it really doesn’t matter what is connected to what as long as new connections are produced. However, if a network is already highly connected then extra links won’t make much difference.]
c. Irreversibility - You never get a second chance
Complex adaptive networks cannot go back and try again. All behaviour is in a sense a one-off ‘experiment’ which can never be repeated. Once a living network has responded to an event the network will have been forever changed, and you cannot undo that adaptation. A judge may say “Will the jury please disregard that statement” but it’s too late.
Equally, any change to a network is contingent (Stephen Jay Gould) on everything that came before. As those conditions can never be exactly recreated, you can never know what would have happened if you had done something else. Rather than thinking in terms of ‘trial and error’, think of a complex adaptive network as being in a continuous process of ‘trial and learning’. This means every moment is a ‘Sliding Doors’ moment.
d. Nonlinearity and fat-tail distributions
We have grown up learning to expect the world to obey two laws: ‘linearity’ and ‘normal’ or bell-shaped frequency distributions. However in complex adaptative networks nonlinearity and power laws or fat-tailed distributions are common:
Linearity has two meanings: ‘sequential’ (in a step-by-step manner) and/or ‘proportional’ (changes in the relationship between two things happen in a straight-line manner — the more you press on the accelerator the faster your car goes and vice versa). This means:
“A big, messy linear problem can always be broken into smaller, more manageable parts. Then each part can be solved separately, and all the little answers can be recombined to solve the bigger problem. So it is literally true that in a linear problem, the whole is exactly equal to the sum of the parts. The hitch, though, is that linear systems are incapable of rich behavior.” Sync, p. 50-1
However, linearity always has limits:
“Most systems behave linearly only when they are close to equilibrium, and only when we don’t push them too hard. When a system goes nonlinear, driven out of its normal operating range, all bets are off. … In any situation where the whole is not equal to the sum of the parts, where things are cooperating or competing, not just adding up their separate contributions, you can be sure that nonlinearity is present. Our nervous system is built from nonlinear components. The laws of ecology are nonlinear. Combination therapy for AIDS patients — drug cocktails — are effective precisely because the immune response and the viral population dynamics are both nonlinear; three drugs taken in combination are much more potent than the sum of the three of them taken separately. Any human psychology is absolutely nonlinear. If you listen to your two favorite songs at the same time you wont get double the pleasure. The synergistic character of nonlinear systems is precisely what makes them so difficult to analyze. They can’t be taken apart. The whole system has to be examined all at once, as a coherent entity. This necessity for global thinking is the greatest challenge to understanding how large systems can spontaneously synchronize themselves. More generally, all problems about self-organization are fundamentally nonlinear.” Sync, p. 181-2
Normal distributions apply to height, weight, athletic capacity, intelligence, etc. They are bell-shaped because they have a distinct peak and tail-off rapidly and equally on both sides. The ‘average’ of a normal distribution is a highly useful piece of information as it immediately tells us a lot about the nature of the system we are dealing with.
However, many networks are organised as a power law or fat-tail distribution. Because we are so used to using the lens of a normal distribution to make sense of the world, networks that obey a power law can display some surprising properties. Firstly, they don’t have a peak and therefore thinking in terms of an ‘average’ isn’t very meaningful. Secondly, the fat-tail means that you are much more likely to find a node with an exceptionally high number of links or interactions than you would expect.
“If the heights of an imaginary planet’s inhabitants followed a power law distribution, most creatures would be really short. But nobody would be surprised to see occasionally a hundred-feet-tall monster walking down the street. In fact, among six billion inhabitants, there would be at least one over 8,000 feet tall. So the distinguishing feature of a power law is not only that there are many small events, but that the numerous tiny events coexist with a few very larger ones. These extraordinary large events are simply forbidden in a bell curve.” Linked, p. 67-68
The size of earthquakes follow a power law and so do many other natural phenomena.
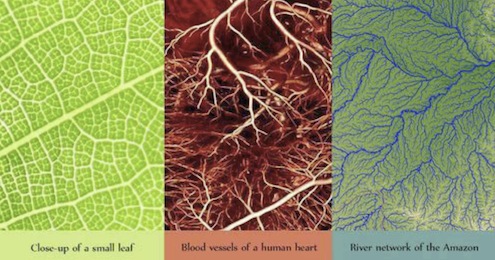
Power-law patterns have another interesting feature. If you magnify any small proportion of say the internet or a river network, it looks much like the whole network. For this to be maintained despite the accidents of history – each of which leave a permanent trace and result in the unique development of every network – means that what happens at one scale is intimately connected with what happens at every other scale. This remarkable self-imposed order is called self-similarity or a fractal.
It is also called a scale-free network because unlike other networks it doesn’t matter at what scale you do your analysis you get the same result.
“The absence of a peak in a power law distribution implies that in a real network there is no such thing as a characteristic node. We see a continuous hierarchy of nodes, spanning from rare hubs to numerous tiny nodes. The power law distribution thus forces us to abandon the idea of a scale, or a characteristic node. There is no intrinsic scale in these networks.” Linked, p. 70
[JL: If mental links follow a power-law, scale-free distribution, it has tremendous implications for modelling and change work.
For example: Hubs and weak links both help to keep the network stable and propagate any changes. As all paths will very quickly lead to a hub, hubs should be fairly easy to find. As should the strong and most used links. Weak links, on the other hand, will not be so obvious as they are rarely used. When a weak link is brought into operation, it may be accompanied by surprise, confusion or an a-ha experience. Or it may be sign-posted by that little something-out-of-the-ordinary that almost goes unnoticed. (What David Grove refers to as a ‘non sequitur’ and Caroline Myss alludes to when she says “The Gods prefer to enter by the backdoor.”)
The power law says there are no typical nodes in scale-free network. Hence groups can be categorised easily but individuals cannot. Yet much of psychology is related to categorising and diagnosing ‘the typical’, e.g. Psychometric tests, and the Diagnostic and Statistical Manual, DSM IV of ‘mental dysfunction’. In Symbolic Modelling while we recognise archetypical patterns, we are most interested in modelling the idiosyncratic and the unique – as identity is a function of the individual as a whole.]
e. Unpredictability - You can't know the outcome in advance
You cannot know how a particular complex network will behave or the precise effect of any particular action because:
The number of permutations (possible pathways) is astronomically large. Ecologists estimated that a proposal by the South African fishing industry to cull the number of seals in the expectation of increasing the catch of hake “would influence the hake population by acting through intermediate species in more than 225 million pathways of cause and effect.” Nexus, p.16
“In life, one cannot simply fast-forward the tape to see what the ending looks like, because the ending is written only in the process of getting there.” Six Degrees, p. 161
Recursion and feedback loops result in nonlinear effects.
At certain points abrupt changes can occur in the network architecture. It is rarely obvious where these thresholds {critical points, tipping points, phase transitions} exist or under what circumstances they will be crossed. The straw that breaks the camel’s back is no different to all the other straws – except that it triggers a nonlinear phenomenon.
Contingency means an event is the outcome of “an unpredictable sequence of antecedent states, where any major change in any step of the sequence would have altered the final result. This final result is therefore dependent, or contingent, upon everything that came before” Nexus, p. 91
The butterfly effect is the idea that in a chaotic system, small disturbances grow exponentially fast, rendering long-term prediction impossible. [Lorenz 1979 paper, ‘Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set off a Tornado in Texas?’] You cannot know which tiny and apparently insignificant events will have consequences out of all proportion to them themselves.
f. Dynamic Equilibrium - You can't have stability without change
As long as a network exists and functions it has to constantly change at a lower level to remain the same at a higher level, i.e. it maintains itself in dynamic equilibrium.
Over the longer term, networks evolve through extended periods of stability and gradual change interspersed by shorter periods of great change and upheaval, i.e. punctuated equilibrium (Stephen Jay Gould).
Complex adaptive networks are inherently resilient and robust. High interconnectivity means in-built fault-tolerance and redundancy. Loosing a number of links will generally not prevent the network from working. Equally, the vast majority of ordinary nodes are not vital to the structural integrity of the network and so their loss has little effect. Taken together it has been estimated that even if half of all nodes on the Internet randomly failed those that remained would still be sewn together in one integrated whole.
However, a co-ordinated attack on certain types of links and nodes is a different matter:
| Robustness and Resilience | Vulnerability and Risk |
| Loosing weak ties that bridge distant clusters will not destroy the network as local groups of nodes can carry on regardless. This is the advantage of modularity. | But, losing a weak tie will reduce the network’s interconnectivity and may result in groups of nodes becoming isolated and being unable to communicate. |
| Hubs bring great connectivity and minimise the effect of loosing a link. The rarity of a hub reduces the possibility of it being the victim of a random event. | But, the loss of a hub may have major consequences for the whole network. This makes them subject to targeted attack. Also, because hubs are so highly connected, a ‘virus’ released into a network will inevitably arrive at a hub which will quickly spread it to a high proportion of the rest of the network. |
Where hubs exist they are key to the functioning of a network, therefore they usually have extra capabilities to deal with problems before, during and after they occur:
- Before – Protection – Your heart is surrounded by a rib cage and big computer sites have all sorts of security.
- During – Redundancy – Extra links mean interactions can continue via a different pathway.
- After – Recovery – Built in repairability and backups mean failures are temporary.
But there are are always consequences. Protecting individual elements in a system may make the whole more vulnerable. The 1996 power outage that plunged the west coast of America into darkness,
“was not a sequence of independent random events that simply aggregated to the point of a crisis. Rather, the initial failure made subsequent failures more likely, and once they occurred, that made further failures more likely still, and so on. … Perhaps the most perturbing aspect of cascading failures is that by installing protective relays on the power generators, by reducing, in effect, the possibility that individual elements of the system would suffer serious damage — the designers had inadvertently made the system as a whole more likely to suffer precisely the kind of global meltdown that occurred.” Six Degrees pp. 23-24
Equally, it is the very interconnectivity of small-world networks that make them vulnerable to the butterfly effect.
The lost of a strong link, a well-used or high activity connection, can either have little effect or potentially set up a dangerous fluctuation. Usually, strong links have lots of alternate pathways – if you can’t get in contact with a good friend one way you probably have many other ways you can reach them. However, if there are very few alternate pathways – e.g. a predator with only a small number of species as prey – then the loss of one strong link can cause an overload in the remaining links and start a cascade which ripples out across the whole network.
Multiple weak links, on the other hand, tend to reduce the effect of fluctuations by dispersing any failure or reduction in effectiveness of any one link to the other remaining links:
“Weak links between species act to take the wind out of dangerous fluctuations. They are the natural pressure valves of ecological communities.” Nexus, p. 150
The effect of removing even one hub can have a dramatic effect because a huge number of weak links will go with it. And, in an ecological community it is not necessarily obvious which are the hubs {keystone species}. They can inconspicuous organisms in the middle of the food chain, basic plants at the bottom of the web, or they might be major predators. By contrast,
“A significant fraction of nodes can be randomly removed from any scale-free network without its breaking apart. This resilience to errors is an inherent property of their topology. …
In scale-free networks, failures predominantly affect the numerous small nodes. Thus, these networks do not break apart under failures. The accidental removal of a single hub will not be fatal either, since the continuous hierarchy of several large hubs will maintain the network’s integrity. Topological robustness is thus rooted in the structural unevenness of scale-free networks. …
[However] the removal of a few hubs [can break a network] into tiny, hopelessly isolated pieces. … Hidden within their structure, scale-free networks harbor an unsuspected Achilles’ heel, coupling a robustness against failures with vulnerability to attack. …
Several of the largest hubs must be simultaneously removed to crush them. This often requires taking out as many as 5 to 15 percent of all hubs at the same time.” Linked, p. 113-118
[JL: In ecosystems the greater the complexity and the greater the diversity (number of species) the less fluctuations and the more stability. However, if change is the desired outcome then more complexity and diversity (of, say, ideas) may make radical change more difficult.
In small worlds, weak links are both change-propagating and change-restraining. They increase the chance of interacting with more ‘distant’ (not alike) nodes. This is particularly important at a time of crisis when, by definition, business-as-usual is not an option. Weak ties increase stability but this in turn works against radical change. At the same time, it is these same weak ties that propagate a change / failure / disease throughout the network.]
g. The rich grow extraordinarily richer - naturally
In certain networks a few hubs can come to dominate the network. The world’s richest three people have assets greater than the combined economic output of the world’s 48 poorest countries (UNHDR 1999).
“The expansion of the network means that the early nodes have more time than the latecomers to acquire links. Thus growth offers a clear advantage to the senior nodes, making them the richest in links. Seniority, however, is not sufficient to explain the power laws. Hubs require the help of the second law, preferential attachment. Because new nodes prefer to link to the more connected nodes, early nodes with more links will be selected more often and will grow faster than their younger and less connected peers. Thus preferential attachment induces a rich-get-richer phenomenon that helps the more connected nodes grab a disproportionate large number of links at the expense of the latecomers.” Linked, p. 87-88
“Preferential attachment makes an additional statement about the way the world works: small differences in ability or even purely random fluctuations can get locked in and lead to very large inequalities over time.” Six Degrees p. 109
Hubs only need to have a small advantage, and either a long time or a lot of activity, to become dominant. However, hubs don’t have things all their own way because dampening feedback loops {self-maintaining, homeostatic or negative feedback} act as a limit to growth of a hub and escalating feedback loops [amplifying, runaway or positive feedback] encourage the growth of smaller nodes.
In either case an aristocratic network will evolve into a more egalitarian network. e.g. A super-sized airport can handle only so many flights before safety, convenience and the law of diminishing returns kicks in. Big companies buy-up smaller companies and become bigger companies until the economies of scale go into decline or the Monopolies Commission steps in.
h. How butterflies cause Tipping Points
A small change in one part of the network can lead to a large change elsewhere in the network or to the whole network – the so-called butterfly effect or to use Malcolm Gladwell’s metaphor, a tipping point. You may be surprised to know that:
“Everything that physicists have discovered indicates that no matter how you bend the rules, there is always a sharp tipping point. … Consequently, even though we know very little, perhaps even next to nothing at all about the psychology and sociology of ideas, mathematical physics guarantees that there is a tipping point.” Nexus, p. 168
[JL: This means there are always conditions under which an individual, a group or a Metaphor Landscape will change. When a system goes beyond a threshold changes occur regardless of individual nodes or links. Of course, whether the change ends up being a breakthrough or a breakdown is another matter.]
These happen through:
A cascade {contagion, chain-reaction, domino-effect} which maintains and propagates the effect of the change across the network. A major fall in one stock market triggers the next market to fall and so on. The addition or removal of one species results in the adaptation of the whole ecosystem.
“[During] an information cascade individuals in populations essentially stop behaving like individuals and start to act more like a coherent mass. Sometimes information cascades occur rapidly [as when a market bubble burst]. And sometimes they happen slowly — new societal norms, like racial equality, woman’s suffrage, and tolerance of homosexuality, for example, can take generations to become [almost] universal.
What all information cascades have in common, however, is that once one commences, it becomes self-perpetuating; that is, it picks up new adherents largely based on the strength of having attracted previous ones. Hence, an initial shock can propagate through a very large system, even if the shock itself is small. Because they are often of a spectacular or consequential nature, cascades tend to make newsworthy events. This disguises the fact that cascades actually happen rather rarely.” Six Degrees p. 205-6
An escalating feedback loop {amplifying, runaway or positive feedback} which keeps amplifying the changes. The effect of a change becomes the new input for the part producing the change (iteration). e.g. 12 rabbits introduced into Australia produced more bunny rabbits which produced … over 600 million. A wildfire creates its own wind which keeps it spreading.
The network being is poised close to a threshold {phase transitions, critical points} e.g. just before the last straw was added that broke the camel’s back. Thresholds are vital because they mark a crisp transition between two completely different network organisations. In some cases, whether a system is one side of a threshold or the other is the only thing matters. There is either a ‘critical mass’ of uranium for a self-propagating chain-reaction or there isn’t and a chain reaction never gets going.
The same seems to be true for whether an infection becomes an epidemic. Thresholds are well known in physics and chemistry: substances melt, evaporate or become solid at very precise points. When a threshold is crossed the system is switching from one network organisation to another, and then the rules of the game change.
“And the key to a [social] cascade is that when making decisions about how to act or what to buy, individuals are influenced not only by their own pasts, perceptions, and prejudices but also but each other.
“One of the most intriguing features of the cascade problem was how most of the time the system is completely stable even in the face of frequent external shocks. But once in a while, for reasons that are never obvious beforehand, one such shock gets blown out of all proportion in the form of a cascade.
“It seemed clear that contagion in a network was every bit as central to the outbreak of cooperation or the bursting of a market bubble as it is to an epidemic of disease. It just wasn’t the same kind of contagion. This is important because typically when we talk about social contagion problems, we use the language of disease.
Thus we speak of ideas as infectious, crime waves as epidemics, and market safeguards as building immunity against financial distress, But the metaphors can be misleading because they suggest that ideas spread from person to person in the same way that diseases do — that all kinds of contagion are essentially the same. They are not. … Social contagion is a highly contingent process.” Six degrees p. 220-224
“Social contagion is even more counterintuitive than biological contagion, because the impact of one person’s actions on another depends on what other influences the latter has been exposed to. The spread of ideas, unlike the spread of disease, requires a trade-off between cohesion within groups and connectivity across them. A node can be vulnerable in one of two ways: either because it has a low threshold (thus, a predisposition to change); or because it possesses only a few neighbours, each of which thereby exert significant influence.” Six Degrees pp. 231-3
[JL: Not only is timing of the introduction of an innovation important, so is where it is introduced. So when in the Maturing Changes phase you enquire if a change to one symbol has spread to another symbol — And when X, what happens to Y? — it may be prudent to start with symbols that are most ‘closely’ connected and move out in ever wider circles. (However, before a change has happened, if you are considering introducing one symbol to another to encourage change — And would X be interested in going to Y — the opposite is usually true, you are offering the network the chance to create a long-distance link.) ]
Often it takes multiple minor contingent events that just happen to happen in close succession to push a system over threshold [cf. my ‘life happens in clumps’ theory].
“Only when a disease reaches a shortcut does it start to display the worst-case, random mixing behavior. Epidemics in a small-world network have to survive first through a slow-growth phase, during which they are most vulnerable. And the lower the density of shortcuts, the longer this slow-growth phase will last.” Six Degrees, p. 181
[JL: While there is a good chance of preventing a full-scale epidemic during the slow-growth phase, when change is the intention, newness and difference will need to be nurtured through the slow-growth phase. This finding supports the notion of (i) Spending time at the beginning of a session to develop the links/relationships in a Metaphor Landscape as this will likely increase the density of shortcuts, thereby shortening the slow-growth phase and (ii) Taking your time at the beginning of the Maturing Changes phase to allow for the completion of the slow-growth phase.]
i. The inverse butterfly effect
A large event or change in one part of the network produces unexpectedly small changes elsewhere. This is dynamic equilibrium at work. i.e the network is robust, resilient or fault-tolerant. This happens when:
The effects of a change are dissipated and absorbed as it travels through the network.
A dampening feedback loop {self-maintaining, homeostatic or negative feedback} counters the effect of the change.
The network has a sufficient requisite variety {a large range of flexibility, spare capacity, float or redundancy} and is far from a threshold so the changes can be compensated within the existing repertoire of responses. The plasticity of brains means that a loss of function can be compensated for by re-routing, rewiring (new links) and/or the growth of new neurones.
The downside is that massive interventions of resources, say aid to developing countries or increased spending on education or the NHS, may not produce much tangible long-term results.
Dampening feedback also helps to prevent egalitarian networks from becoming aristocratic.
At present there is little that limits the number of links to a site on the WWW and so it has rapidly become an aristocratic network. However, whenever putting all your eggs into one basket becomes too much of a risk of creating a giant omelette a more egalitarian distribution will result.
“The cascading failure that struck the West [Coast of the US and causes a massive blackout] on August 10, 1996, was not a sequence of independent random events that simply aggregated to the point of a crisis. Rather, the initial failure made subsequent failures more likely, and once they occurred, that made further failures more likely still, and so on. …
Perhaps the most perturbing aspect of cascading failures is that by installing protective relays on the power generators, by reducing, in effect, the possibility that individual elements of the system would suffer serious damage — the designers had inadvertently made the system as a whole more likely to suffer precisely the kind of global meltdown that occurred.” Six Degrees p. 23-24
[JL: A great example of when a solution becomes a problem.]
“There are three ways in which cascades can be forbidden. The first one is obvious: if everyone’s threshold is too high, no one will ever change and the system will remain stable regardless of how it is connected. Even when this is not the case, cascades can still be forbidden by the network itself, in two ways: either it is not well connected enough or (and this is the surprising part) it is too well connected.
Networks that are not connected enough, therefore, prohibit global cascades because the cascade has no way of jumping from one vulnerable cluster to another. And networks that are too highly connected prohibit cascades also, but for a different reason: they are locked into a kind of stasis, each node constraining the influence of any other and being constrained itself. In social contagion, a system will only experience global cascades if it strikes a trade-off between local stability and global connectivity.” Six Degrees p. 237 & 241
“In scale-free networks even if a [computer] virus is not very contagious, it spreads and persists. Defying all wisdom accumulated during five decades of diffusion studies, viruses travelling in scale-free networks are practically unstoppable. The source of this unexpected behavior lies in the uneven topology. Scale-free networks are dominated by hubs.
Because each hub is linked to a very large number of other [nodes], it has a high chance of being [re-]infected by one of them. Once infected, a hub can pass on the virus to all the other [nodes] it is linked to. Thus highly linked hubs offer a unique means by which viruses persist and spread. ” Linked, p. 135
[JL: This maybe one way to explain why ‘relapse’ after an apparently successful relief from depression or anxiety is not uncommon. If an unproductive thought (a ‘thought virus’ as Robert Dilts calls them) survives somewhere on the network it has a good chance of eventually re-infecting nodes that have become virus-free. And re-infection may come from outside (i.e. from another part of the network of which the client is a part). This metaphor suggests that, rather than attempting to the eliminate all negative thoughts, it maybe wiser to establish a way of handling them when they occur, i.e. building up an immunity.]
4. Further Reading
Philip Ball, Critical Mass: How one thing leads to another (2004)
Albert-László Barabasi, Linked: How everything is connected to everything else (2003).
Albert-László Barabási: Web Without a Spider: The Emergence of Complex Networks, Video recording of a lecture given March 4, 2003 at MIT
Albert-László Barabasi, Linked: Networks from Biology to the World Wide Web, Video/audio recording of a lecture given September 27, 2005 at Wellesley College, USA.
Mark Buchanan, Nexus: Small worlds and the science of networks (2002)
Fritjof Capra, The Web of Life: A new synthesis of mind and matter (1996)
Fritjof Capra, Hidden Connections: Integrating the biological, cognitive and social (2002)
Malcolm Gladwell, The Tipping Point: How little things can make a big difference (2002)
Steven Johnson, Emergence: The connected lives of ants, brains, cities and software (2001)
Steven Strogatz, Sync: Rhythms of nature, rhythms of ourselves (2003)
James Surowiecki, The Wisdom of Crowds: Why the many are smarter than the few (2005)
Mark Ward, Universality: The underlying theory behind life, the universe and everything
Duncan Watts, Six Degrees: The Science of a connected age (2003)